4.1 Video Motion Analysis (Using Tracker software)
Trial 1: Pre-Modification Trial
Trial 2-3: Post-Modification Trail
Foreword:
Analysing distance-time, velocity-time and acceleration-time graphs generated from the videos of the mousetrap cars allows us to evaluate whether the modifications made had succeeded in improving performance, and to highlight the areas of improvements.
TRIAL 1
4.1.1.1 Displacement–time graph
4.1.1.2 Velocity–time graph
4.1.1.3 Acceleration–time graph 
TRIAL 2
4.1.2.1 Displacement–time graph
4.1.2.2 Velocity–time graph
4.1.2.3 Acceleration–time graph 
TRIAL 3
4.1.3.1 Displacement–time graph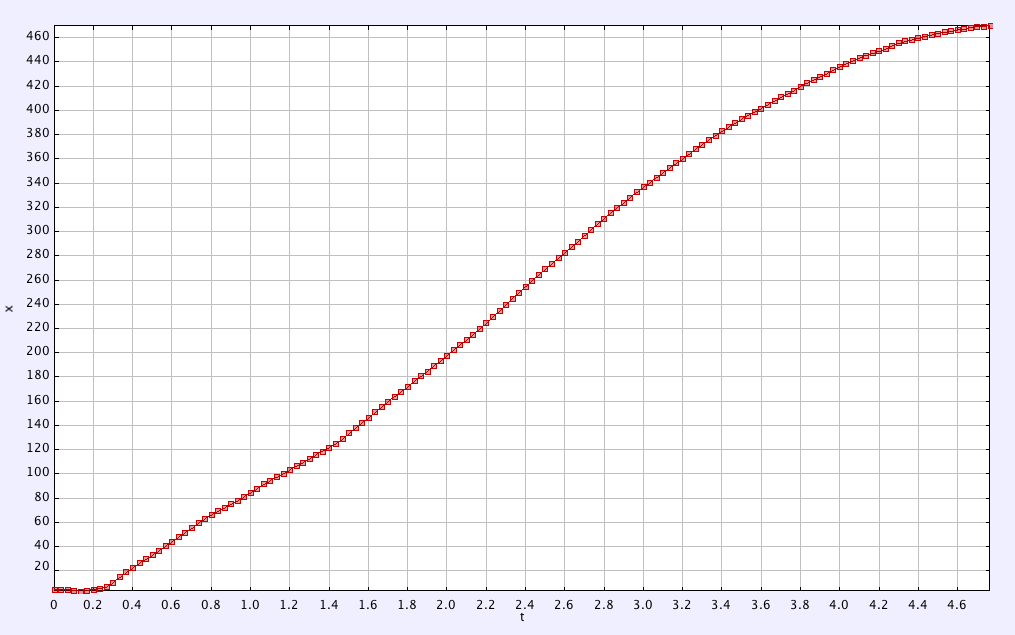
4.1.3.2 Velocity–time graph
4.1.3.3 Acceleration–time graph 
4.2 Data Analysis
4.2.1. Which wheels are you drive wheels?
The rear wheels are the driving wheels of the car.
4.2.2. What is the circumference of your drive wheels?
The circumference of the car’s drive wheels is 37.7cm (3s.f.)
4.2.3. How far will your car travel in one rotation of the drive wheels?
Since the circumference of the drive wheels is 37.7cm, one full rotation of the wheel will allow the car to travel a distance of 37.7cm.
4.2.4. How many rotations (on average ) were there in each run?
On average there was around 19 rotations per run.
4.2.5. How much string is used in one rotation of the drive wheels? Show how you calculated this.
Amount of string used in 1 rotation = circumference of axle = 2 x π x 0.25cm = 1.57cm (3.sf.)
4.2.6. The release of the lever is the power stroke. What is the length of your vehicles power stroke? (Length of string released)
Post-modification: Power stroke = 32.0cm
4.2.7. Calculate how far your vehicle will travel during the power stroke. Show your calculations.
Power stroke = 32cm
Length of string used per rotation = 1.57cm
No. of rounds = 32 ÷ 1.57 ≈ 20 (0 d.p.)
Circumference of wheel = 37.7cm
37.7 x 20 rounds = 754 cm = 7.54m
∴Distance vehicle will travel = 7.54m
4.2.8. Compare the answer to 4.2.7 to the distance your measured during your car’s power stroke. Discuss possible reasons for different valuables.
The difference in distance travelled may be affected by the improper alignment of the wheels. Because the wheels are slightly tilted in, this slowed down the car and could have affected the performance of the mousetrap car.
4.2.9. Calculate the average velocity for your car during the period after the spring fully releases.
Average velocity = (v-u)/2
= (2.20-0)/2
= 1.10 m s-1
4.2.10. What force causes your car to stop?
The car starts to slow down and stopped because of the frictional force acting on the wheels as the car travels.
4.2.11. The work done by a force is calculated by multiplying the force times the distance over which it acts. The work done on an object is equal to the change in its kinetic energy.
- Can you find a way to calculate the force of friction? Use equations and explain your steps. HINT: Be careful, you have calculated average velocity.
- How can you find the total amount of kinetic energy (immediately after spring release) if we assume the acceleration during coasting was constant?
I) Let KEC be the kinetic energy of the car.
Let FR be the resultant force, FA be the applied force, and FF be the friction force.
Work done = FR × Distance
∴ Work done = KEC
KEC = ½ mv2
KEC = ½ (0.425)(1.1)2
KEC = 0.257J
KEC = 0.2575.5
KEC = 1.4135 J
∵ KEC = FR × Distance
FR = 1.4135/5.5
= 0.25 N
FA = Mass × Acceleration
= (0.425) x 2.20/3.4s
= 0.275 N
∵ FF = FA - FR
∴ FF = 0.275 - 0.25
= 0.025N
II)
Let KEI be the initial kinetic energy after spring release.
KEI = FA × Distance
= 0.275 x 3 (distance car travels while power stroke is releasing)
= 0.825J
4.2.12. Various experiments have been done to measure the potential energy
available from the spring. One estimate is 0.65 Joules. Using your estimates
of the maximum kinetic energy of your car and the work done by friction,
discuss whether or not this is a reasonable value. Can you account for any
differences in the forms of energy? You must justify all of your arguments.
During the trial of the mousetrap car, many unaccountable external factors are due to affect the way the car travels. This may have either caused it to move further than calculated, or move a smaller distance than predicted. At the same time, the calculations are based on the values obtained from a trial run of the mousetrap car, making complete accuracy impossible. As the question stated, the “one estimate” is 0.65J. It therefore could be entirely possible that 0.65J is completely valid, thus it is reasonable.
No comments:
Post a Comment